Όπως είδαμε και στην ενότητα «Εισαγωγή στα διαμάντια», το διαμάντι, εκτός του ότι είναι ένα ορυκτό, ανήκει και στην κρυσταλλική ύλη. Δηλαδή είναι ανόργανο σώμα που ακολουθεί συγκεκριμένους και ακλόνητους κόμβους δόμησης και πλήρωσης του χώρου.
Το 98% των ορυκτών είναι κρύσταλλοι και, γιʼ αυτόν το λόγο, συνήθως οι όροι ορυκτό και κρύσταλλος είναι συνώνυμοι.
Τα ορυκτά είναι φυσικά στερεά σώματα, ανόργανες χημικές ενώσεις που δημιουργούνται με γεωλογικές και γεωχημικές διαδικασίες στο εσωτερικό της γης. Η χημική τους σύσταση είναι σταθερή, η δομή τους είναι κρυσταλλική και οι φυσικές τους ιδιότητες είναι συγκεκριμένες και αμετάβλητες. Τα ορυκτά επίσης αποτελούν συστατικά των πετρωμάτων, και τα πετρώματα, όπως είναι γνωστό, δομούν τον στερεό φλοιό της Γης (τη λιθόσφαιρα). Η χημική σύσταση των ορυκτών μπορεί να είναι πολύ απλή – μπορεί να αποτελείται από ένα μόνο στοιχείο, μπορεί να είναι απλό άλας ή οξείδιο, ή σύνθετες και περίπλοκες χημικές ενώσεις.
Πριν ξεκινήσουμε την ορυκτολογική περιγραφή του διαμαντιού, θα κάνουμε μια σύντομη αναφορά στην κρυσταλλογραφία και στην ισοτροπία.
Είπαμε ότι τα ορυκτά είναι κρύσταλλοι οι οποίοι δομούνται με αυστηρούς και συγκεκριμένους κανόνες. Η συμμετρία όμως των κρυστάλλων δεν είναι αυθαίρετη, αλλά συγκεκριμένη. Δηλαδή όλα τα ορυκτά κρυσταλλώνονται σε επτά κρυσταλλικές ομάδες. Η κάθε ομάδα από αυτές έχει καθορισμένη συμμετρία, την οποία ακολουθούν όσοι κρύσταλλοι κρυσταλλώνονται σε αυτή την ομάδα. Οι κρυσταλλικές αυτές ομάδες ονομάζονται κρυσταλλογραφικά συστήματα και, όπως είπαμε, είναι επτά. Για παράδειγμα, ένα από αυτά είναι το τριγωνικό σύστημα, στο οποίο κρυσταλλώνονται ο χαλαζίας (αμέθυστος, καπνίας, ροζ χαλαζίας), τα κορούνδια (ρουμπίνια, ζαφείρια) κ.ά. Ένα άλλο κρυσταλλογραφικό σύστημα είναι το εξαγωνικό, του οποίου τη συμμετρία ακολουθεί η βήρυλλος (σμαράγδι, ακουαμαρίνα). Επίσης υπάρχει το ρομβικό σύστημα, στο οποίο ανήκει το τοπάζι.
Τα επτά κρυσταλλογραφικά συστήματα (crystal systems) είναι:
- Τρικλινές (τιρκουάζ)
- Μονοκλινές (φεγγαρόπετρα)
- Ρομβικό (περίδοτο)
- Τετραγωνικό (ζιρκόνιο)
- Τριγωνικό (τουρμαλίνης)
- Εξαγωνικό (απατίτης)
- Κυβικό (γρανάτες)
Καθένα από τα παραπάνω κρυσταλλικά συστήματα έχει διαφορετική συμμετρία από τα υπόλοιπα. Επειδή τα δομικά συστατικά των κρυστάλλων είναι τα ιόντα των χημικών στοιχείων, και επειδή αυτά τα ιόντα, όπως είπαμε, κατέχουν συγκεκριμένες θέσεις και ακολουθούν αυστηρή συμμετρία, όλα αυτά επιφέρουν σημαντικές επιπτώσεις στις φυσικές ιδιότητές τους.
Για παράδειγμα, το φως δεν συμπεριφέρεται το ίδιο στο τρικλινές σύστημα, σε σχέση με τη συμπεριφορά που έχει στο τριγωνικό κρυσταλλικό σύστημα. Ένα σώμα μπορεί να είναι, σε ό,τι αφορά το φως, ισότροπο ή ανισότροπο. Ισότροπο σημαίνει ότι το φως μέσα σε αυτό έχει πάντα σταθερή ταχύτητα, ενώ ανισότροπο, ότι το φως δεν έχει σταθερή ταχύτητα, αλλά η ταχύτητά του εξαρτάται από τη διεύθυνση.
Από τα επτά κρυσταλλικά συστήματα μόνο το κυβικό είναι ισότροπο, τα υπόλοιπα έξι είναι ανισότροπα συστήματα. Δηλαδή, στην περίπτωση των κρυστάλλων που κρυσταλλώνονται με βάση τη συμμετρία του κυβικού, η ταχύτητα του φωτός μέσα σε αυτούς είναι σταθερή. Στα υπόλοιπα έξι συστήματα το φως έχει μία μέγιστη και μία ελάχιστη τιμή. Παράδειγμα, στο διαμάντι το φως έχει πάντα ταχύτητα 124.000 km/sec, ενώ στο ρουμπίνι η ταχύτητα του φωτός κυμαίνεται από 169.000 km/sec έως 170.000 km/sec.
Όπως μόλις αναφέραμε, το διαμάντι κρυσταλλώνεται στο ισότροπο κυβικό σύστημα. Θα μπορούσαμε να πούμε ότι το κυβικό κρυσταλλικό σύστημα δομεί τον χώρο με απόλυτη συμμετρία και ισότητα. Και αυτό γιατί η δόμηση ακολουθεί τρεις ισοδύναμους άξονες συμμετρίας προς τις τρεις διαστάσεις του χώρου, κάτι που δεν συμβαίνει στα υπόλοιπα κρυσταλλογραφικά συστήματα, τα οποία έχουν έναν εξέχοντα άξονα συμμετρίας (σχήμα 1 και 2). Από πολύ νωρίς κάνουμε την διαπίστωση ότι ο λίθος αυτός διαθέτει εκ φύσεως πληρότητα και σταθερότητα. Δηλαδή η φύση τον κατατάσσει σε ομάδα συμμετρίας που του δίνει ισοτροπία και ταυτόχρονα απόλυτη συμμετρία γύρω από το κέντρο του κρυστάλλου του.

Σχήμα 1: Βλέπουμε τους τρεις κύριους ισχυρούς άξονες συμμετρίας στη στοιχειώδη κυψελίδα του κυβικού κρυσταλλογραφικού συστήματος. Παρατηρούμε ότι η κατανομή της ύλης στον χώρο είναι ισοδύναμη και προς τις τρεις διαστάσεις.
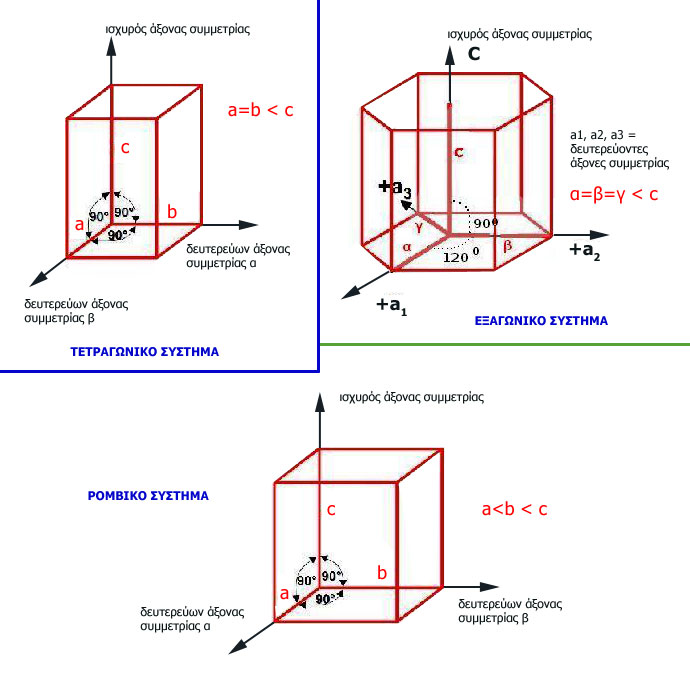
Σχήμα 2.: Παρατηρούμε τις στοιχειώδεις κυψελίδες και τους άξονες συμμετρίας στα τρία αυτά κρυσταλλογραφικά συστήματα (τετραγωνικό, εξαγωνικό και ρομβικό). Βλέπουμε πώς, σε αντίθεση με το κυβικό σύστημα, υπάρχουν σε αυτά άξονες συμμετρίας που είναι πιο ισχυροί από άλλους. Αυτό έχει ως αποτέλεσμα τη δημιουργία διευθύνσεων πυκνότερης συγκέντρωσης της ύλης. Η ύλη όμως που δομεί τους κρυστάλλους είναι κατά κανόνα ιόντα. Έτσι, πυκνότερα ιόντα προς μία κατεύθυνση σημαίνει και ανισότροπη συμπεριφορά στην ηλεκτρομαγνητική ακτινοβολία.

Σχήμα 3.

Φωτογραφία 1: Κρύσταλλος διαμαντιού όπως απαντά στη φύση (οκτάεδρο).

Φωτογραφία 2: Σύνθετος κρύσταλλος διαμαντιού.
Όμως η τελειότητα του διαμαντιού δεν σταματά εδώ. Το κάθε κρυσταλλογραφικό σύστημα διαθέτει υποομάδες. Συγκεκριμένα το κυβικό σύστημα έχει πέντε υποομάδες που τις ονομάζουμε κρυσταλλογραφικές τάξεις. Οι πέντε αυτές τάξεις του κυβικού δεν έχουν όλες την ίδια συμμετρία. Η πρώτη τάξη, που ονομάζεται ολοεδρία, συγκεντρώνει την πλήρη συμμετρία του κρυσταλλογραφικού συστήματος, ενώ οι υπόλοιπες τέσσερις είναι πιο φτωχές σε στοιχεία συμμετρίας. Δηλαδή η ολοεδρία του κυβικού διαθέτει δεκατρείς (13) άξονες συμμετρίας και εννέα (9) επίπεδα συμμετρίας. Οι υπόλοιπες τέσσερις τάξεις δεν διαθέτουν όλα αυτά τα στοιχεία συμμετρίας. Βλέπουμε δηλαδή ότι και μέσα στο κυβικό σύστημα, πάλι το διαμάντι υπερέχει, διότι διαθέτει όλο τον πλούτο της συμμετρίας. Ξανά όμως, όσο απίστευτο κι αν σας φαίνεται, η τελειότητα και ο πλούτος του διαμαντιού δεν τελειώνει ούτε εδώ, αλλά συνεχίζει ακόμα και σε πιο μικρή κλίμακα, φτάνοντας μέχρι και σε ατομικό επίπεδο.
Είδαμε ότι υπάρχουν επτά κρυσταλλογραφικά συστήματα, που το καθένα χαρακτηρίζεται από τη δική του ξεχωριστή συμμετρία. Εκτός από τη διαφορετική συμμετρία των επτά αυτών συστημάτων, τα συστήματα διαφέρουν και σε κάτι ακόμα πιο βασικό. Το κάθε σύστημα διαθέτει το δικό του διαφορετικό δομικό «τουβλάκι» με το οποίο χτίζονται οι κρύσταλλοί του. Το μικροσκοπικό αυτό τουβλάκι ονομάζεται στοιχειώδης κυψελίδα. Στο κυβικό σύστημα η στοιχειώδης κυψελίδα είναι ο κύβος. Όποιο κι αν είναι το ορυκτό που κρυσταλλώνεται στο κυβικό σύστημα και σε όποια από τις πέντε κρυσταλλογραφικές του τάξεις, οι κρύσταλλοί του χτίζονται με μικροσκοπικά κυβάκια (σχήμα 3 και φωτ. 1).
Σε αυτήν τώρα τη στοιχειώδη κυψελίδα οι δομικές μονάδες, τα ιόντα των στοιχείων δηλαδή, κατέχουν συγκεκριμένες θέσεις, όπως είδαμε και στην ενότητα «Εισαγωγή στα διαμάντια». Δηλαδή ο κύβος παραχωρεί ειδικές θέσεις όπου μπορούν να καθίσουν τα άτομα ή τα ιόντα των στοιχείων – δεν υπάρχει χάος και αναρχία αλλά απόλυτη τάξη. Στο κυβικό σύστημα και στη στοιχειώδη κυψελίδα του, υπάρχουν τρεις τρόποι πλήρωσης του χώρου. Αυτά τα αυστηρά καθορισμένα σημεία όπου μπορούν να τοποθετηθούν οι δομικές μονάδες του κρυστάλλου ονομάζονται πλεγματικά σημεία. Μόνο σε αυτά τοποθετούνται τα άτομα του στοιχείου που αποτελεί τη χημική σύσταση του ορυκτού. Εάν η χημική σύσταση είναι πολύπλοκη, τότε δεν χωράνε όλα τα άτομα και τα ιόντα στα πλεγματικά σημεία, γιʼ αυτό τα πλεγματικά σημεία είναι μαθηματικά σημεία που δηλώνουν τη δυνατότητα ύπαρξης ιόντων και ατόμων σε αυτά
Πάμε τώρα να δούμε τους τρεις τρόπους πλήρωσης του χώρου στο κυβικό σύστημα. Η στοιχειώδης κυψελίδα, το κυβάκι, επιτρέπει να «καθίσουν» χημικές μονάδες δόμησης:
α) στις κορυφές του κύβου, στην απλή στοιχειώδη κυψελίδα
β) στις κορυφές του κύβου και στο κέντρο του, στη χωροκεντρωμένη κυψελίδα
γ) στις κορυφές του κύβου και στα μέσα των εδρών του, στις ολοεδρικά κεντρωμένες κυψελίδες. (σχήμα 4)
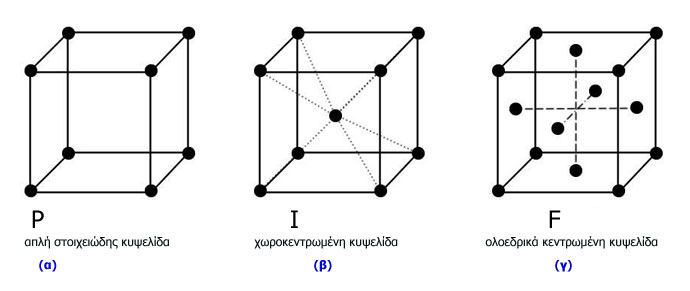
Σχήμα 4.
Από όλους αυτούς τους τρόπους δόμησης του χώρου, υπάρχει ο απλός τρόπος (α), ο ενδιάμεσος (β) και ο τρίτος ο πιο πλήρης. Ποιος λέτε λοιπόν ότι θα είναι ο τρόπος που το διαμάντι θα γεμίζει τον χώρο με τα άτομα του άνθρακα; Καλά μαντέψατε, ο τρίτος, ο πιο πλήρης. Ακόμα δηλαδή και στην κλίμακα της στοιχειώδους κυψελίδας, το διαμάντι διαφέρει από τη συντριπτική πλειοψηφία των ορυκτών.

Σχήμα 5.
Συνοψίζοντας, το διαμάντι κρυσταλλώνεται στην ολοεδρία του κυβικού συστήματος και έχει ολοεδρικά κεντρωμένη κυψελίδα. Οι κρυσταλλικές μορφές με τις οποίες εμφανίζεται συνήθως στη φύση το διαμάντι είναι το οκτάεδρο, το δωδεκάεδρο και συνδυασμοί των δύο αυτών κρυσταλλικών σχημάτων (σχήμα 5 και φωτ. 1,2). Η ακμή του κύβου της στοιχειώδους κυψελίδας του διαμαντιού είναι 0,356 nm. Ο στοιχειομετρικός του αριθμός Z = 8. Ο Z μας δείχνει πόσες φορές η χημική σύσταση του ορυκτού χωρά μέσα στη στοιχειώδη κυψελίδα του. Δηλαδή στο μικροσκοπικό κυβάκι με διάσταση 0,356 nm, που χτίζει τους κρυστάλλους του διαμαντιού, βρίσκονται οκτώ άτομα άνθρακα (σχήμα 6).

Σχήμα 6: Σχηματική απεικόνιση της στοιχειώδους κυψελίδας του διαμαντιού και των θέσεων που καταλαμβάνουν σε αυτήν τα άτομα του άνθρακα.
Ως κρύσταλλος θα έχει και σταθερή χημική σύσταση. Είναι πασίγνωστο ότι η χημική του σύσταση είναι πολύ απλή και αποτελείται από ένα μόνο χημικό στοιχείο, θα λέγαμε ίσως το πιο σύνηθες χημικό στοιχείο, τον άνθρακα (C).
Η σκληρότητά του, που και αυτή είναι πασίγνωστη, έχει στη σχετική κλίμακα του Mohs (σκληρομετρική κλίμακα Μος), τη μέγιστη τιμή 10. Σε πολλά ορυκτολογικά εγχειρίδια, θα βρείτε γραμμένο ότι το διαμάντι είναι το πιο σκληρό από τα υλικά που γνωρίζει ο άνθρωπος. Εγώ θα συμπληρώσω ότι είναι το πιο σκληρό υλικό στο σύμπαν.
Ο δείκτης διάθλασής του είναι 2,42, αρκετά υψηλός, το ειδικό του βάρος είναι 3,52, είναι δηλαδή 3,5 φορές πιο βαρύ από το νερό. Η λάμψη του είναι αδαμαντώδης. Η διάχυση του φωτός είναι 0,057, πολύ υψηλή τιμή. Στην γεμολογία η τιμή της διάχυσης (dispersion) μας δείχνει την ένταση με την οποία το λευκό φως αναλύεται στα επτά γνωστά μας χρώματα της ίριδας καθώς εισέρχεται στον κρύσταλλο.
Ας δούμε πάλι πιο αναλυτικά τις φυσικές ιδιότητες του διαμαντιού και τις κρυσταλλοχημικές του παραμέτρους.
Σίγουρα παραπάνω σας δημιουργήσαμε σύγχυση και απορίες, διότι υποπέσαμε σε αντιφάσεις και σφάλματα. Στο σχήμα 4 περιγράφουμε και απεικονίζουμε την κυβική ολοεδρικά χωροκεντρωμένη στοιχειώδη κυψελίδα. Εκεί σαφέστατα φαίνεται ότι σε αυτήν μπορούν να τοποθετηθούν 14 άτομα άνθρακα. Οκτώ, ένα σε κάθε κορυφή του κύβου, συν 6 άτομα άνθρακα ακόμα, στα κέντρα των έξι εδρών του. Αμέσως μετά αναφέρουμε ότι ο στοιχειομετρικός αριθμός Z του διαμαντιού είναι 8. Δηλαδή ότι στην κάθε στοιχειώδη ολοεδρικά κεντρωμένη κυψελίδα του διαμαντιού χωράνε 8 άτομα άνθρακα. Στη συνέχεια, στο σχήμα 6 φαίνεται να υπάρχουν 18 άτομα άνθρακα εντός της κυψελίδας. Τελικά τι ακριβώς συμβαίνει και ποιος είναι ο ακριβής αριθμός των ατόμων άνθρακα που υπάρχουν στη στοιχειώδη κυψελίδα του διαμαντιού;
Όλα τα παραπάνω είναι αληθινά, διότι το διαμάντι σπάει τους νόμους και «αναγκάζει» τη φύση να κάνει εξαίρεση, χωρίς όμως να χαλάσει τη συμμετρία και την τάξη της. Αυτό που απεικονίζεται στο σχήμα 4 είναι η πραγματικότητα, δηλαδή πράγματι 14 άτομα άνθρακα χωράνε στη στοιχειώδη κυψελίδα. όμως, όπως φαίνεται στο σχήμα 3, η κάθε στοιχειώδης κυψελίδα δεν είναι μόνη της, αλλά πάντα μαζί με άπειρες άλλες χτίζει τον κρύσταλλο. Έτσι, τα άτομα του άνθρακα που είναι στις κορυφές ανήκουν ταυτόχρονα σε οκτώ στοιχειώδεις κυψελίδες, επομένως ανήκουν κατά το 1/8 μόνο στην κάθε κυψελίδα (γιʼ αυτό και στο σχήμα 6 τα έχουμε με το ίδιο χρώμα). Το συμπέρασμα είναι ότι, εφόσον υπάρχουν 8 άτομα στις κορυφές, αλλά ανήκουν κατά το 1/8 στην κυψελίδα, στην πραγματικότητα μόνο 1 ανήκει σε αυτήν. Τα άτομα που βρίσκονται στα μέσα των εδρών ανήκουν σε δύο γειτονικές κυψελίδες, ανήκουν δηλαδή κατά το ήμισυ στην κάθε κυψελίδα. Εφόσον έχουμε έξι άτομα που βρίσκονται στα μέσα των εδρών, άρα μόνα τρία ανήκουν στην κάθε κυψελίδα (πάλι στο σχήμα 6 απεικονίζονται με ίδιο χρώμα τα άτομα που βρίσκονται σε απέναντι έδρες). Τελικά δηλαδή έχουμε ένα άτομο από τις κορυφές και τρία άτομα από τα μέσα των εδρών = τέσσερα (4) άτομα άνθρακα ανά στοιχειώδη κυψελίδα.
Δηλαδή στη φύση όσα ορυκτά κρυσταλλώνονται στο κυβικό κρυσταλλογραφικό σύστημα και έχουν ολοεδρικά χωροκεντρωμένη στοιχειώδη κυψελίδα, πρέπει να έχουν στοιχειομετρικό αριθμό Z = 4. Πράγματι αυτό συμβαίνει με το χρυσό, το ασήμι, το θείο, την πλατίνα, τον γαληνίτη, τον αλίτη, τον φθορίτη και τόσα άλλα ορυκτά. Γιατί όμως δεν συμβαίνει το ίδιο και με το διαμάντι;
Όπως πάντα, το διαμάντι αποτελεί εξαίρεση, ευχάριστη και ευεργετική όμως. Είπαμε ότι συνήθως οι κρύσταλλοι χτίζονται από ιόντα. Στο διαμάντι τα άτομα του άνθρακα δεν είναι ιόντα και δεν συνδέονται με τον ιοντικό δεσμό. Ιόν σημαίνει ότι λείπει ή λείπουν ηλεκτρόνια από ένα στοιχείο ή ότι έχει παραπάνω ηλεκτρόνια από το κανονικό. Τα άτομα του άνθρακα στο διαμάντι έχουν τα φυσιολογικά ηλεκτρόνια, δεν έχουν δηλαδή ηλεκτρικό φορτίο, έτσι δεν γίνεται να αναπτύξουν ιοντικό δεσμό. Συνδέονται μεταξύ τους με έναν άλλο χημικό δεσμό, τον ομοιοπολικό. Σύμφωνα με αυτόν, όλα τα άτομα του άνθρακα μοιράζονται συνολικά τον ίδιο αριθμό ηλεκτρονίων. Έτσι κάθε άτομο άνθρακα συνδέεται με άλλα τέσσερα άτομα σχηματίζοντας ένα τετράεδρο, που στο κέντρο του βρίσκεται ένα άτομο άνθρακα και στις κορυφές του, τα τέσσερα άτομα άνθρακα που μοιράζονται τα ηλεκτρόνια μαζί του στον ομοιοπολικό δεσμό (σχήμα 7).
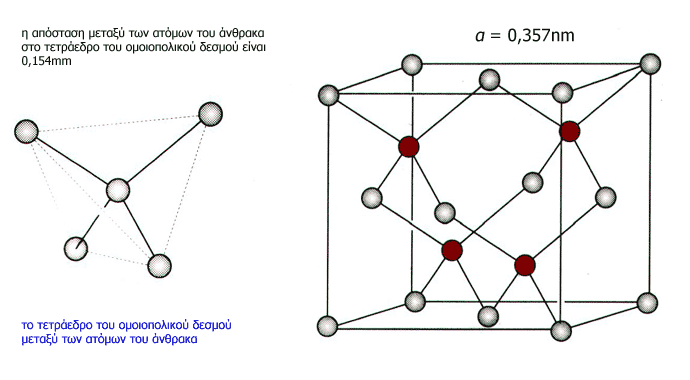
Σχήμα 7.
Σύμφωνα με τα παραπάνω, πρέπει στη στοιχειώδη κυψελίδα του διαμαντιού να βρίσκονται 14 άτομα άνθρακα σύμφωνα με το σχήμα 4. Ταυτόχρονα όμως το κάθε άτομο άνθρακα λόγω του ομοιοπολικού δεσμού πρέπει να βρίσκεται και στο κέντρο ενός τετραέδρου, σύμφωνα με το σχήμα 7. Αυτά τα δύο αναγκάζουν την ολοεδρικά χωροκεντρωμένη κυψελίδα του κυβικού κρυσταλλογραφικού συστήματος να φιλοξενήσει τέσσερα (4) άτομα άνθρακα παραπάνω από το φυσιολογικό. Έτσι τελικά στην πραγματικότητα έχουμε 18 άτομα άνθρακα, όπως δείχνει το σχήμα 6. Τα τέσσερα αυτά επιπλέον άτομα βρίσκονται στο εσωτερικό της κυψελίδας (γκρίζα στο σχήμα 6 και κόκκινα στο σχήμα 7), ανήκουν δηλαδή εξ ολοκλήρου σε αυτήν.
Να λοιπόν πως καταλήγουμε στο Z = 8. Από τα 14 άτομα του σχήματος 4, είπαμε πως μόνο τα 4 ανήκουν στην κάθε στοιχειώδη κυψελίδα, τα άλλα τέσσερα που στριμώχνονται κι αυτά εκεί λόγω του ομοιοπολικού δεσμού, εφόσον είναι μέσα στην κάθε στοιχειώδη κυψελίδα ανήκουν ολόκληρα σε αυτήν. Επομένως έχουμε 4 + 4 = 8.
Σε αυτήν ακριβώς την αιτία οφείλεται και η εξαιρετική σκληρότητα του διαμαντιού. Δηλαδή ο ομοιοπολικός δεσμός είναι ένας πολύ ισχυρός δεσμός, πιο ισχυρός από τον ιοντικό, διότι ο ιοντικός μπορεί να εξασθένησει εάν επιδράσουν σε αυτόν ισχυρά φορτία, κάτι που δεν συμβαίνει στον ομοιοπολικό, μιας και στον ομοιοπολικό δεν έχουμε ιόντα. Πρώτον, λοιπόν, στο διαμάντι τα άτομα του άνθρακα συνδέονται με έναν πολύ ισχυρό δεσμό, και δεύτερον με πολύ πυκνή δομή, εφόσον στη στοιχειώδη κυψελίδα του, υπάρχουν 4 παραπάνω άτομα από αυτά που προβλέπει η φύση! Αυτή λοιπόν η ισχυρή και συνεκτική κρυσταλλοχημική δομή δεν μπορεί εύκολα να σπάσει και να χαλάσει. Μακροσκοπικά και σε μεγάλη κλίμακα, το αποτέλεσμα όλων αυτών είναι η ακραία σκληρότητα του διαμαντιού.
Όταν χαράζουμε έναν κρύσταλλο, στην πραγματικότητα προκαλούμε καταστροφή στο κρυσταλλικό του πλέγμα. Καταλαβαίνετε πως κάτι τέτοιο δεν γνωρίζουμε έως τώρα να μπορεί να συμβεί στην περίπτωση του κρυσταλλικού πλέγματος του διαμαντιού. Πιστεύω, ύστερα από όλα αυτά, να μην εξακολουθεί να σας φαίνεται υπερβολή αυτό που παραπάνω γράψαμε, ότι δηλαδή το διαμάντι είναι το σκληρότερο υλικό στο σύμπαν. Οι νόμοι της φύσης είναι παγκόσμιοι και δεν έχουν μόνον τοπική εφαρμογή. Δηλαδή, ο τρόπος που συνδέονται τα άτομο και τα μόρια ισχύει από τη μια άκρη του σύμπαντος στην άλλη. Ένας τέτοιος δεσμός που επικρατεί στο κρυσταλλοχημικό πλέγμα του διαμαντιού δεν νομίζω ότι εύκολα θα ξεπεραστεί κάπου στο σύμπαν, όσο απέραντο κι αν είναι αυτό. Η πυκνή δομή του κρυστάλλου του διαμαντιού εξηγεί και το υψηλό του ειδικό βάρος. Ο άνθρακας, με ατομικό βάρος 12, είναι ένα από τα ελαφρύτερα στοιχεία, και όμως το ειδικό του βάρος (3,52) είναι τρεισήμισι φορές πιο μεγάλο από το ειδικό βάρος του νερού. Δεν θα μπορούσε να είναι κι αλλιώς εφόσον η «γέμιση» της στοιχειώδους κυψελίδας του διαμαντιού είναι η διπλάσια από αυτήν που προβλέπει η φύση. Για μία φορά ακόμα, η κρυσταλλοχημεία του ευθύνεται και για την επόμενη ακραία φυσική του ιδιότητα, η οποία μας δίνει όλες τις υπέροχες οπτικές ιδιότητες. Φυσικά μιλάμε για τον υψηλότατο δείκτη διάθλασής του (2,42). Το φως ως ηλεκτρομαγνητική ακτινοβολία δεν είναι τίποτε άλλο από μια ταλάντωση. Όταν αυτή λοιπόν η ταλάντωση συναντήσει την πυκνή κρυσταλλική δομή του διαμαντιού, θα βρει αντίσταση και ως συνέπεια θα χάσει την κινητική του ενέργεια, δηλαδή θα υποστεί επιβράδυνση (μείωση της ταχύτητας του φωτός μόλις εισέλθει στο διαμάντι).
Τι είπαμε για τον δείκτη διάθλασης (δ.δ.) στο κεφάλαιο της ολικής εσωτερικής ανάκλασης; Όσο πιο μεγάλος είναι ο δ.δ. ενός υλικού, τόσο περισσότερο μειώνεται η ταχύτητά του όταν το φως εισέλθει σε αυτό. Και το αντίστροφο, όσο ο δ.δ. είναι κοντά στην μονάδα, τόσο λιγότερο μειώνεται η ταχύτητα του φωτός όταν εισέρχεται σε αυτό το οπτικό μέσο. Η τιμή 2,42 είναι πάρα πολύ υψηλή, γεγονός που σημαίνει ότι μειώνεται δραματικά η ταχύτητα του φωτός μέσα σʼ ένα διαμάντι.
Τα υλικά που έχουν μεγάλο δ.δ. έχουν κατά κανόνα και ισχυρή λάμψη, και ευνοείται σε αυτά η διάχυση του φωτός, η ανάλυση δηλαδή του φωτός στα συστατικά του χρώματα. Αυτά ακριβώς χαρακτηρίζουν τον κρύσταλλο αυτό: ισχυρή αδαμαντώδης λάμψη και υψηλή διάχυση (dispersion). Και οι δύο αυτές ιδιότητες τον κάνουν πανέμορφο και μοναδικό.
Ύστερα από όλα αυτά επιμένετε ακόμα ότι το διαμάντι μπορεί να προκύψει από τα κάρβουνα;! (Θυμηθείτε τι γράψαμε στο κεφάλαιο«η χρησιμότητα του διαμαντιού στην επιστήμη»). Το διαμάντι, αυτό το θαύμα της φύσης που συνίσταται αποκλειστικά από άνθρακα, ένα στοιχείο που στη συντριπτική πλειοψηφία των χημικών του ενώσεων δίνει πλαστικότητα και χαμηλή σκληρότητα (οργανικές ενώσεις, πλαστικά κ.λπ.), εδώ προικίζεται από τη φύση με τα εντελώς αντίθετα χαρακτηριστικά, την απόλυτη τάξη και ακαμψία και την αδιαφιλονίκητη θέση στο ψηλότερο σκαλί του βάθρου της σκληρότητας.




 © 2016 - 2024. All Rights Reserved
© 2016 - 2024. All Rights Reserved




